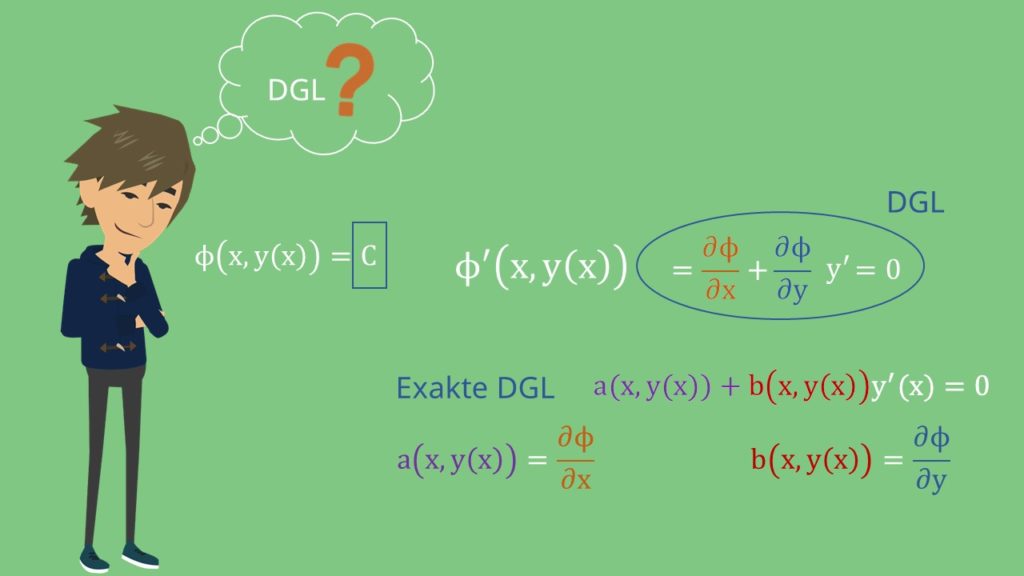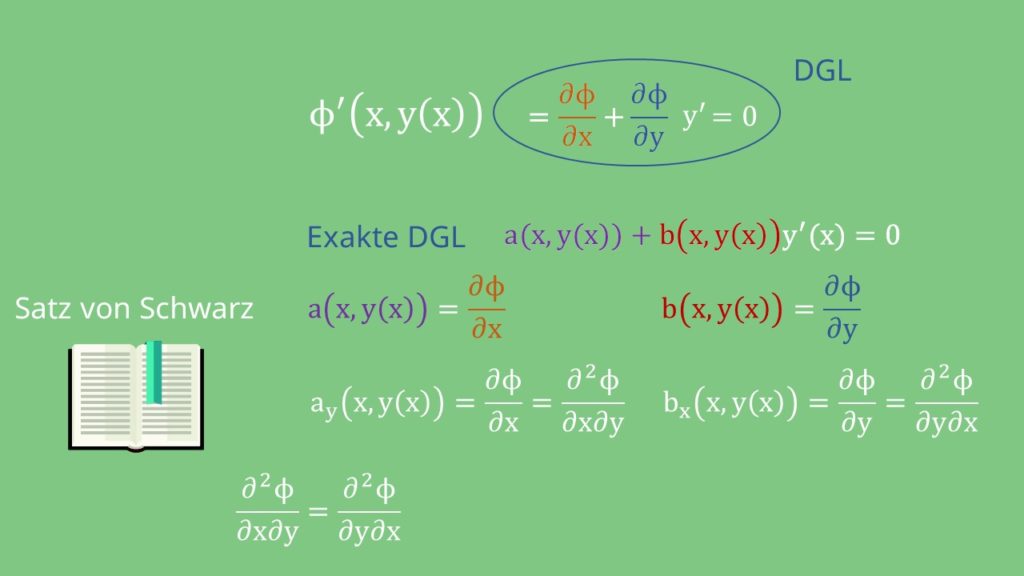Exakte DGL
Du möchtest wissen, was eine Exakte DGL ist und wie du sie lösen kannst? Im Folgenden zeigen wir dir das Vorgehen bei diesen speziellen Differenzialgleichungen an einem einfachen Beispiel.
Inhaltsübersicht
Exakte Differentialgleichung: Potentialkonstruktion
Zunächst schauen wir uns die Grundidee und zwar die Konstruktion eines Potentials an:

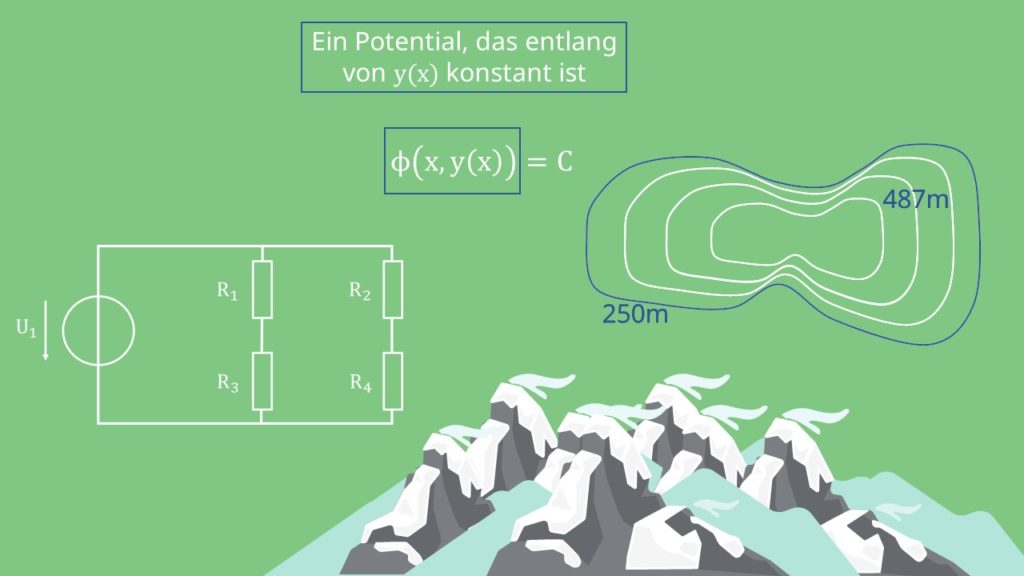
 ist eine Potentialfunktion, die entlang von
ist eine Potentialfunktion, die entlang von  konstant ist. Du kannst sie dir wie eine konstante Höhe im Gebirge vorstellen. Entlang der Höhenlinie bist du auf demselben Potential. Ein gleiches Spannungsniveau im elektrischen Schaltkreis wäre ebenfalls ein Beispiel dafür.
konstant ist. Du kannst sie dir wie eine konstante Höhe im Gebirge vorstellen. Entlang der Höhenlinie bist du auf demselben Potential. Ein gleiches Spannungsniveau im elektrischen Schaltkreis wäre ebenfalls ein Beispiel dafür.
Die Konstante  kannst du mithilfe eines Anfangswertes bestimmen.
kannst du mithilfe eines Anfangswertes bestimmen.
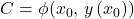
Schließlich kann man die Gleichung eindeutig nach y auflösen, um eine Lösung zu erhalten.
Herleitung der Integrabilitätsbedingung
Du fragst dich, wo hier jetzt eine Differentialgleichung steckt? Dazu leiten wir  ab. Zunächst bilden wir die partielle Ableitung nach
ab. Zunächst bilden wir die partielle Ableitung nach  und danach nach
und danach nach  , die wir noch mit der inneren Ableitung, also
, die wir noch mit der inneren Ableitung, also  multiplizieren müssen. Auf der rechten Seite der Gleichung für
multiplizieren müssen. Auf der rechten Seite der Gleichung für  steht eine Konstante, deren Ableitung Null ist.
steht eine Konstante, deren Ableitung Null ist.

Schon hat sich eine DGL ergeben. Nun ersetzen wir die partiellen Ableitungen von  durch die Funktionen
durch die Funktionen  und
und  .
.

Eine exakte DGL muss genau diese Form haben. Vergleichst du diese mit dem vorherigen Ausdruck, stellst du fest, dass folgende Teile übereinstimmen.


 ist die partielle Ableitung von
ist die partielle Ableitung von  und
und  die partielle Ableitung nach
die partielle Ableitung nach  .
.
Jetzt leitest du nochmal nach der jeweils anderen Variable ab.


Nach dem Satz von Schwarz kann in der zweiten Ableitung die Reihenfolge der partiellen Ableitungen vertauscht werden, sodass die gemischten Ableitungen einander entsprechen.

Schreiben wir das nun wieder als  und
und  :
:

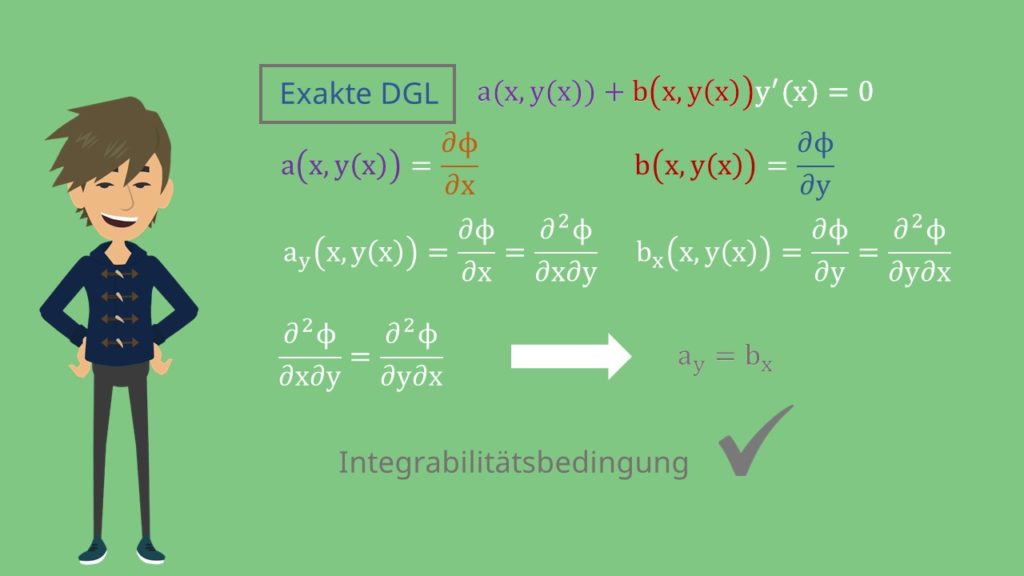
Wir haben uns eine Bedingung für Exaktheit hergeleitet. Sie heißt Integrabilitätsbedingung. Ist diese Bedingung erfüllt, haben wir eine exakte DGL.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Exakte DGL – Beispiel
Soweit zur Theorie. Es wird Zeit für ein Beispiel

Du hast diese Gleichung vor dir liegen und vergleichst sie mit der allgemeinen Form,

um  und
und  zu bestimmen. Nun prüfst du die Integrabilitätsbedingung, indem du zuerst
zu bestimmen. Nun prüfst du die Integrabilitätsbedingung, indem du zuerst  nach
nach  ableitest.
ableitest.  abgeleitet nach
abgeleitet nach  ergibt Null und
ergibt Null und  abgeleitet nach
abgeleitet nach  ergibt
ergibt  . Dann leitest du noch
. Dann leitest du noch  nach
nach  ab.
ab.  y nach
y nach  abgeleitet ergibt
abgeleitet ergibt  , die Konstante 1 fällt beim Ableiten raus. Du stellst fest,
, die Konstante 1 fällt beim Ableiten raus. Du stellst fest,

dass die Integrabilitätsbedingung erfüllt ist.  ist gleich
ist gleich  . Daraus kannst du folgern, dass deine DGL exakt ist.
. Daraus kannst du folgern, dass deine DGL exakt ist.
Das Potential kannst du auf verschiedene Arten konstruieren. Die erste Möglichkeit ist, dass du  nach
nach  integrierst,
integrierst,

da wir  als
als  definiert haben.
definiert haben.

Außerdem intergierst du  entsprechend seiner Definition als
entsprechend seiner Definition als  nach
nach  .
.
Die Integrationskonstanten  und
und  sind jeweils von der Variablen
sind jeweils von der Variablen  oder
oder  abhängig, nach der nicht integriert wurde.
abhängig, nach der nicht integriert wurde.
Zurück zum Beispiel: Wir integrieren  nach
nach 

Das ergibt

Als nächstes integrieren wir  nach
nach  .
.
Jetzt vergleichen wir die Integrale:

Du erkennst den Mischterm  in beiden Integralen. Der Anteil
in beiden Integralen. Der Anteil  ist nur von
ist nur von  abhängig und entspricht somit der Integrationskonstante
abhängig und entspricht somit der Integrationskonstante  . Analog dazu ist
. Analog dazu ist  gleich
gleich  .
.
Es ergibt sich

Ganz wichtig ist, dass du die Integrale vergleichst und nicht einfach beide Integrale addierst. Sonst nimmst du den Mischterm doppelt ins Ergebnis auf und das ist falsch.
Kommen wir jetzt noch zur zweiten Möglichkeit um  zu ermitteln. Sie erfordert weniger Integrierarbeit, allerdings musst du dich mehr konzentrieren, um den Überblick zu behalten.
zu ermitteln. Sie erfordert weniger Integrierarbeit, allerdings musst du dich mehr konzentrieren, um den Überblick zu behalten.
Nach der ersten Integration
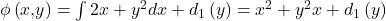
kannst du das Ergebnis auch nach der anderen Variablen ableiten und anschließend mit  vergleichen.
vergleichen.
Der Mischterm  taucht auf beiden Seiten auf und außerdem ist
taucht auf beiden Seiten auf und außerdem ist  . Integriert nach
. Integriert nach  ergibt sich
ergibt sich  . Das führt ebenfalls zum Ergebnis
. Das führt ebenfalls zum Ergebnis

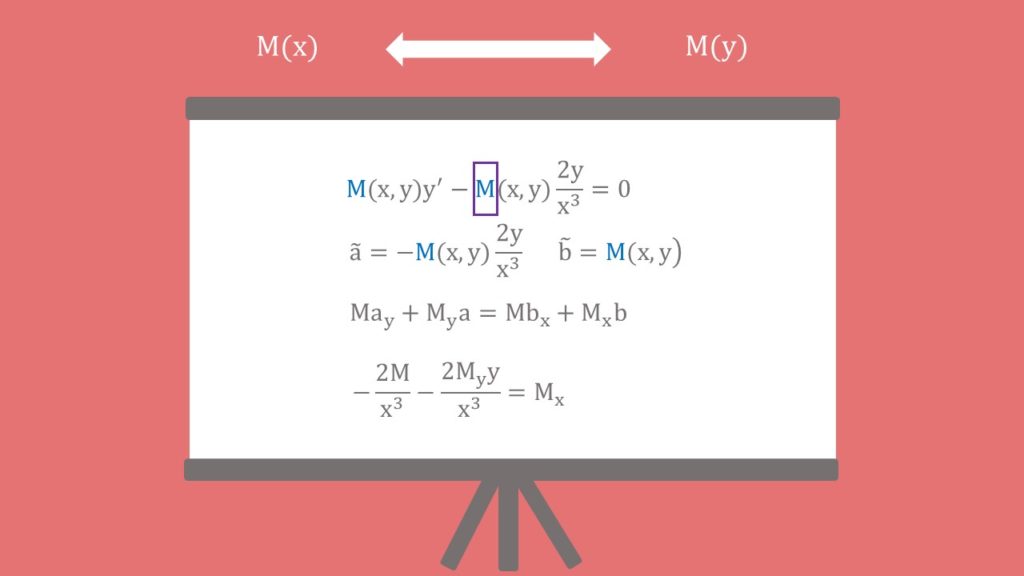
Transformation zu exakten Differentialgleichungen
Manche Differentialgleichungen, die nicht exakt sind, kannst du mit einem integrierenden Faktor multiplizieren, so dass sie zu exakten Differentialgleichungen werden. Nehmen wir diese Beispiel-DGL

und bestimmen  und
und 


Diese leiten wir ab und sehen, dass die Integrabilitätsbedingung nicht erfüllt ist. Also multiplizierst du die DGL mit einem 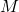 und bestimmst
und bestimmst  und
und  .
.
Leitest du sie ab und setzt sie gleich, erhältst du diese Gleichung

Darin setzt du noch das Beispiel ein

Der Trick ist, ein 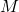 zu wählen, dass nur von einer Variable abhängt. Dadurch erzeugst du eine einfache gewöhnliche DGL, mit der du
zu wählen, dass nur von einer Variable abhängt. Dadurch erzeugst du eine einfache gewöhnliche DGL, mit der du 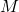 bestimmen kannst. Ob du ein
bestimmen kannst. Ob du ein  oder ein
oder ein  wählst, ist dir überlassen. Du musst ausprobieren, wie du eine zielführende bzw. die einfachere DGL erzeugst.
wählst, ist dir überlassen. Du musst ausprobieren, wie du eine zielführende bzw. die einfachere DGL erzeugst.
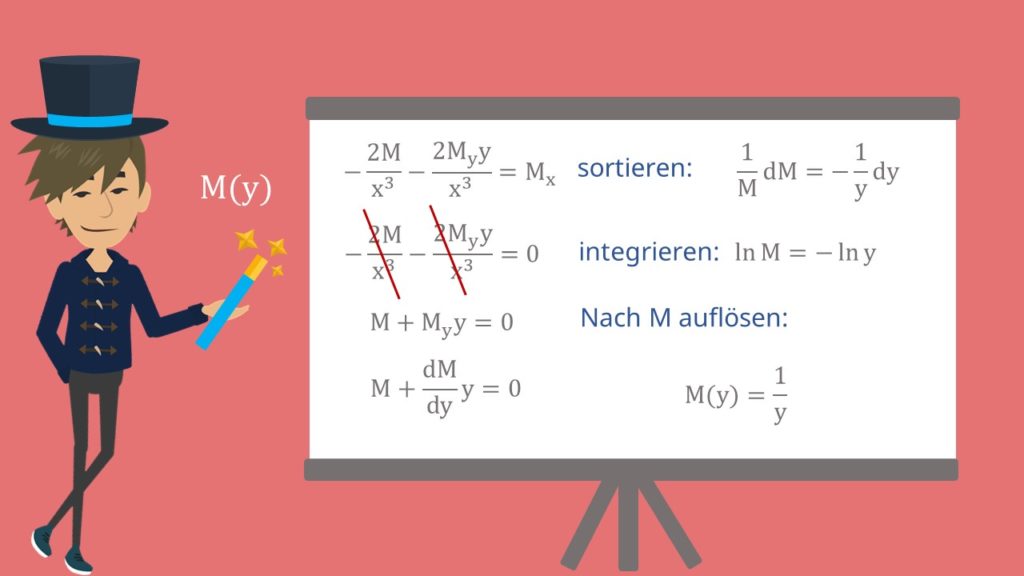
Probieren wir mal  . Die Ableitung
. Die Ableitung  fällt raus
fällt raus
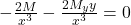
Jetzt kannst du  rauskürzen. Die DGL löst du mit Trennung der Variablen. Dann sortierst du erst mal, um danach zu integrieren und nach
rauskürzen. Die DGL löst du mit Trennung der Variablen. Dann sortierst du erst mal, um danach zu integrieren und nach 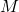 aufzulösen. Es ergibt sich
aufzulösen. Es ergibt sich  .
.
Jetzt machen wir noch die Probe, indem wir  und
und  auf Integrabilität prüfen.
auf Integrabilität prüfen.
Für  ergibt sich:
ergibt sich:
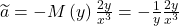
Nun setzt du für  ein und das
ein und das  kürzt sich raus.
kürzt sich raus.  ist leicht zu bestimmen. Jetzt kannst du
ist leicht zu bestimmen. Jetzt kannst du  nach
nach  ableiten, was null ergibt, und
ableiten, was null ergibt, und  nach
nach  ableiten. Das ergibt ebenfalls Null. Die Integrabilitätsbedingung ist also erfüllt.
ableiten. Das ergibt ebenfalls Null. Die Integrabilitätsbedingung ist also erfüllt.

Abschließend könntest du das Potential bestimmen. Die Vorgehensweise haben wir weiter oben schon erklärt. Jetzt weißt du wie man beim Lösen einer exakten Differentialgleichung vorgeht.