Wellengleichung
In diesem Beitrag zeigen wir dir, wie du die Wellengleichung mit dem Separationsansatz löst.
Inhaltsübersicht
Wellengleichung lösen
Die Wellengleichung beschreibt die Ausbreitung von Wellen. Das können zum Beispiel Schallwellen, Wasserwellen oder elektromagnetische Wellen sein. Es handelt sich um eine hyperbolische Differentialgleichung. Die eindimensionale Wellengleichung sieht so aus:

Die Funktion u beschreibt die Auslenkung der Welle, die sich in Raum und Zeit ändert. c ist die Wellenausbreitungsgeschwindigkeit. Wir setzen den Produktansatz

in die Differentialgleichung ein

und ziehen die Terme, nach denen nicht abgeleitet wird, aus den Ableitungen.

Als Nächstes schreiben wir die Gleichung kompakter
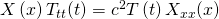
und separieren alle x-Anteile und alle t-Anteile voneinander.

Jetzt können wir beide Seiten der Konstanten  gleichsetzen
gleichsetzen

und erhalten zwei gewöhnliche Differentialgleichungen zweiter Ordnung


Werfen wir jetzt mal einen Blick auf die Randbedingungen.
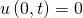
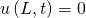
Wir können aus den beiden Randbedingungen folgern, dass X von Null und X von Eins Null sind.


Anfangsbedingungen Wellengleichung Formel
Die Anfangsbedingungen sehen wie folgt aus. Wir haben die Anfangsauslenkung und ihre Ableitung nach der Zeit gegeben.
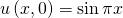

Aber mit diesen beschäftigen wir uns später. Die x-abhängige Differentialgleichung und die Randbedingungen für groß X erinnern stark an die Wärmeleitungsgleichung.

Daher kürzen wir das Sturm-Liouville-Problem etwas ab und wählen direkt den Ansatz:

Wir wählen wieder ein Alpha,

um die Darstellung der Lösung übersichtlicher zu gestalten. In diese

setzen wir die Randbedingungen für X ein.

Aus X von Null folgt, dass  gleich Null ist
gleich Null ist

Und der Sinus von Alpha muss ebenfalls Null sein

Daher muss \alpha ein Vielfaches von n\pi sein. Für \lambda ergibt sich damit folgender Ausdruck.

Dafür haben wir die Definition von  nach
nach  umgestellt und
umgestellt und  durch
durch  ersetzt.
ersetzt.
Das Ergebnis für Lambda können wir jetzt auch in die Lösung für T einsetzen.


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Imaginäre Eigenwerte
Das charakteristische Polynom sieht so aus

und führt auf die Eigenwerte

Imaginäre Eigenwerte bedeuten, dass die Lösung eine trigonometrische Reihe ist, also aus Sinus- und Kosinus-Funktionen besteht.

Jetzt kannst du die Gesamtlösung zusammensetzen

und die Konstanten zusammenfassen.

 mal
mal  wird zu
wird zu  und
und  mal
mal  wird zu
wird zu  .
.
Nun kannst du die Anfangsbedingungen einsetzen.

Vergleichst du die Koeffizienten, erhältst du  und die restlichen
und die restlichen  .
.
Um die Konstanten  Schalnge zu bestimmen, brauchen wir die zweite Anfangsbedingung. Wir leiten u nach t ab und setzen t gleich Null in die Ableitung ein
Schalnge zu bestimmen, brauchen wir die zweite Anfangsbedingung. Wir leiten u nach t ab und setzen t gleich Null in die Ableitung ein

Also ist
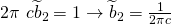
 gleich Eins und
gleich Eins und  ergibt sich zu
ergibt sich zu  . Die restlichen Koeffizienten sind
. Die restlichen Koeffizienten sind 
Die Gesamtlösung ist also diese hier:

Alle Konstanten  und
und 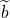 sind verschwunden. Achte unbedingt darauf, dass du auch in den Argumenten des Sinus und Kosinus alle n‘s einsetzt. Du hast den Separationsansatz erfolgreich auf eine weitere Differentialgleichung, die Wellengleichung, angewendet.
sind verschwunden. Achte unbedingt darauf, dass du auch in den Argumenten des Sinus und Kosinus alle n‘s einsetzt. Du hast den Separationsansatz erfolgreich auf eine weitere Differentialgleichung, die Wellengleichung, angewendet.


