Video

Quiz

Hier geht's zum Video „Abstand Gerade Gerade“

Hier geht's zum Video „Schnittpunkt zweier Geraden“

Abstand windschiefer Geraden

Wichtige Inhalte in diesem Video

Abstand windschiefer Geraden einfach erklärt

Abstand windschiefer Geraden Formel

Abstand windschiefer Geraden mit laufenden Punkten

In diesem Beitrag erklären wir dir, wie du den Abstand zweier windschiefer Geraden berechnen kannst. Du findest schrittweise Rechnungsanleitungen und passende Beispiele zur Berechnung mit Hilfe der Formel und der Lotfußpunktverfahren.

Für eine kurze und anschauliche Erklärung der Abstandsberechnung kannst du dir auch unser Video zum Thema Abstand windschiefer Geraden ansehen.

Inhaltsübersicht

Abstand windschiefer Geraden einfach erklärt

im Videozur Stelle im Video springen

Zwei Geraden bezeichnet man als windschief, wenn sie keinen gemeinsamen Schnittpunkt besitzen und nicht parallel zueinander stehen. Genauer stehen zwei Geraden windschief zueinander, wenn

ihre Richtungsvektoren keine Vielfachen voneinander sind
bei der Bestimmung des Schnittpunkts eine falsche Aussage entsteht (es existiert kein Schnittpunkt).

Reicht es zur Lösung einer Aufgabe aus, nur den Abstand zu berechnen, dann können wir ganz einfach den Formelansatz anwenden. Wird jedoch neben der Distanz zwischen den Geraden auch die Bestimmung der Punkte auf den Geraden verlangt, an denen diese sich am nächsten kommen, rechnen wir am besten mit einem der Lotfußpunktverfahren.

Im Folgenden erklären wir dir nacheinander alle drei Lösungswege und rechnen jeweils ein ausführliches Beispiel durch.

Abstand windschiefer Geraden Formel

im Videozur Stelle im Video springen

Die Abstandsformel der Geraden macht immer dann Sinn, wenn nur nach dem Abstand gefragt ist. Die Koordinaten der Punkte auf den Geraden, in denen diese sich am nächsten kommen, berechnet man hierbei nicht. Gesucht ist der Abstand der windschiefen Geraden $g: \vec{x} = \vec{p} + \lambda \vec{u}$ und $h: \vec{x} = \vec{q} + \phi \vec{v}$ .

Abstandsformel windschiefer Geraden

$d = \frac{\vert (\vec{q} - \vec{p}) \cdot \vec{n} \vert}{\vert \vec{n} \vert}$

$\vec{q}$ : Vektor des Aufpunktes von
$\vec{p}$ : Vektor des Aufpunkts von
$\vec{n}$ : Normalenvektor $\vec{n}$ $(= \vec{u} \times \vec{v})$

Um die kürzeste Distanz zwischen zwei windschiefen Geraden mit der Abstandsformel zu bestimmen, musst du folgende Rechenschritte durchgehen:

Anleitung Formel

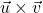Normalenvektor $\vec{n}$ mit Hilfe des Kreuzproduktes ( $\vec{u} \times \vec{v}$ ) berechnen
Vektor $\vec{p}$ von Vektor $\vec{q}$ abziehen. Ergebnis ist der Verbindungsvektor $\vec{PQ}$
Skalarprodukt aus $\vec{PQ}$ und $\vec{n}$ bilden
Betrag des Skalarprodukts durch Betrag von $\vec{n}$ teilen

Beispielaufgabe – Formel

Wir suchen den Abstand der Geraden und .

$g: \vec{x} = \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right)$

$h: \vec{x} = \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) + \phi \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right)$

Zur Berechnung der Formel müssen wir zunächst den Normalenvektor $\vec{n}$ der beiden Geraden berechnen. Dazu bilden wir das Vektorprodukt der beiden Richtungsvektoren.

$\vec{u} \times \vec{v} = \left( \begin{array}{c} u_2 v_3 - u_3 v_2 \\\ u_3 v_1 - u_1 v_3 \\\ u_1 v_2 - u_2 v_1 \\\ \end{array}\right) = \left( \begin{array}{c} 1 \cdot 1 - 2 \cdot 2 \\\ 2 \cdot (-1) - 0 \cdot 1 \\\ 0 \cdot 2 - 1 \cdot (-1) \\\ \end{array}\right) = \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right)$

$\vec{n} = \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right)$

Jetzt können wir den Normalenvektor und die Aufpunkte der Geradengleichungen in die Formel der Abstandsberechnung einsetzen.

$d = \frac{\Biggl | \Biggl[ \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) - \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) \Biggr] \cdot \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right) \Biggl |}{\Biggl | \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right) \Biggl |} = \frac{\Biggl | \left( \begin{array}{c} 2 \\\ -1 \\\ 1 \\\ \end{array}\right) \cdot \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right) \Biggl |}{\Biggl | \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right) \Biggl |} \\ = \frac{\vert -6 + 2 + 1 \vert}{\sqrt{(-3)^2+(-2)^2+1^2}}$

An dieser Stelle müssen die Beträge bestimmt und danach geteilt werden. Als Ergebnis erhalten wir einen Abstand von rund 0,8 LE zwischen den windschiefen Geraden.

$d = \frac{\vert -3 \vert}{\sqrt{14}} = \frac{3}{\sqrt{14}} \approx 0,8$

Abstand windschiefer Geraden mit Hilfsebene

Der Berechnungsweg mit Hilfe einer Hilfsebene entspricht einem der beiden Lotfußpunktverfahren . Im Vergleich zur Formel erhält man über die Hilfsebene zusätzlich zur Entfernung der Geraden auch die Punkte, in denen sich die Geraden am nächsten kommen. Die Hilfsebene wählen wir dabei so, dass sie eine der Geraden enthält und ihr zweiter Richtungsvektor (siehe Grafik: $\vec{n}$ ) senkrecht auf den Richtungsvektoren beider Geraden steht.

Anleitung Hilfsebene

Den Abstand der windschiefen Geraden $g: \vec{x} = \vec{p} + \lambda \vec{u}$ und $h: \vec{x} = \vec{q} + \phi \vec{v}$ lässt sich folgendermaßen berechnen:

Bestimmung des Vektors $\vec{n}$ , der senkrecht auf beiden Richtungsvektoren steht ( $\vec{n} = \vec{u} \times \vec{v}$ )
Konstruktion einer Hilfsebene $E_g: \vec{x} = \vec{p} + \lambda \vec{u} + \omega \vec{n}$
Berechnung der Lotfußpunkte (Schnittpunkte) und 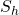der Ebene mit den Geraden und
Bestimmung des Abstands der windschiefen Geraden: $d = \vert \vec{S_g S_h} \vert$

Abstand windschiefer Geraden, Windschiefe Geraden, Lotfußpunktverfahren mit Hilfsebene — Lotfußpunktverfahren mit Hilfsebene

Beispiel „Hilfsebene“

Weiterhin ist der Abstand der Geraden und gesucht.

$g: \vec{x} = \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right)$

$h: \vec{x} = \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) + \phi \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right)$

1. $\vec{n}$ bestimmen

Um einen Vektor zu erhalten, der auf beiden Richtungsvektoren der Geraden senkrecht steht, bilden wir das Vektorprodukt aus $\vec{u}$ und $\vec{v}$ .

$\vec{n} = \vec{u} \times \vec{v} = \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right) \times \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right) = \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right)$

2. aufstellen

Mit Hilfe des Vektors $\vec{n}$ und der Geradengleichung von können wir jetzt die Gleichung der Hilfsebene E_g aufstellen.

$E_g: \vec{x} = \vec{p} + \lambda \vec{u} + \omega \vec{n} = \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right) + \omega \cdot \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right)$

3. Lotfußpunkte berechnen

Da wir die Ebene E_g im vorherigen Schritt so definiert haben, dass sie die Gerade enthält, bestimmen wir nun den Schnittpunkt der Ebene mit . Hierzu setzt man Ebenen- und Geradengleichung gleich.

E_g = h

$\left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right) + \omega \cdot \left( \begin{array}{c} -3 \\\ -2 \\\ 1 \\\ \end{array}\right) = \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) + \phi \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right)$

Die Zeilen können wir nun in ein Gleichungssystem mit drei Unbekannten umwandeln.

$I \ 1 + 0 \lambda - 3 \omega = 3 - 1 \phi$
$II \ 4 + 1 \lambda - 2 \omega = 3 + 2 \phi$
$III \ 2 + 2 \lambda + 1 \omega = 3 + 1 \phi$

Nach mehreren Auflösungsschritten erhalten wir ein $\phi$ von $\frac{19}{14}$ . Dieser Wert kann anschließend in die Geradengleichung eingesetzt werden und liefert uns dann den Lotfußpunkt S_h .

$\vec{s_h} = \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) + \frac{19}{14} \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right) = \left( \begin{array}{c} \frac{23}{14} \\\\ \frac{40}{7} \\\\ \frac{61}{14} \\\ \end{array}\right)$

$S_h \ (\frac{23}{14} \vert \frac{40}{7} \vert \frac{61}{14})$

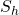Um den Fußpunkt auf der Gerade ermitteln zu können, lösen wir das Gleichungssystem nach $\lambda$ auf. Für $\lambda$ ergibt sich ein Wert von $\frac{9}{7}$ . Eingesetzt in die Geradengleichung erhalten wir den Schnittpunkt S_g .

$\vec{s_g} = \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \frac{9}{7} \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right) = \left( \begin{array}{c} 1 \\\\ \frac{37}{7} \\\\ \frac{32}{7} \\\\ \end{array}\right)$

$S_g \ (1 \vert \frac{37}{7} \vert \frac{32}{7})$

4. Länge des Vektors $\vec{S_g S_h}$ bestimmen

Zunächst berechnen wir den Verbindungsvektor der beiden Lotfußpunkte auf den Geraden.

$\vec{S_g S_h} = \vec{s_h} - \vec{s_g} = \left( \begin{array}{c} \frac{23}{14} \\\\ \frac{40}{7} \\\\ \frac{61}{14} \\\\ \end{array}\right) - \left( \begin{array}{c} 1 \\\\ \frac{37}{7} \\\\ \frac{32}{7} \\\\ \end{array}\right) = \left( \begin{array}{c} \frac{9}{14} \\\\ \frac{3}{7} \\\\ -\frac{3}{14} \\\\ \end{array}\right)$

Der gesuchte Abstand der windschiefen Geraden entspricht jetzt dem Betrag dieses Verbindungsvektors der beiden Lotfußpunkte.

$d(g, h) =\vert \vec{S_g S_h} \vert = \sqrt{\frac{9}{14}^2 + \frac{3}{7}^2 + (-\frac{3}{14})^2} \approx 0,8$

Abstand windschiefer Geraden mit laufenden Punkten

im Videozur Stelle im Video springen

Bei dem Lotfußpunktverfahren mit laufenden Punkten berechnen wir zugleich den Abstand und die Punkte auf den windschiefen Geraden, in denen die Distanz minimal ist. Die kürzeste Verbindungslinie muss auf beiden Geraden zugleich senkrecht stehen. Das heißt der minimale Verbindungsvektor (siehe Grafik: $\vec{S_h S_g}$ ) multipliziert mit den jeweiligen Richtungsvektoren der Geraden ergibt Null. Mit Hilfe dieses Gleichungssystems lassen sich die Lotfußpunkte bestimmen und wir können den Abstand zweier windschiefer Geraden ausrechnen.

Anleitung laufende Punkte

Den Abstand der windschiefen Geraden $g: \vec{x} = \vec{p} + \lambda \vec{u}$ und $h: \vec{x} = \vec{q} + \phi \vec{v}$ lässt sich folgendermaßen berechnen:

Aufstellen des allgemeinen Verbindungsvektors $\vec{S_g S_h}$ , der die Parameter der beiden windschiefen Geraden enthält
Gleichungssystem aus den Bedingungen $\vec{S_g S_h} \cdot \vec{u} = 0$ und $\vec{S_g S_h} \cdot \vec{v} = 0$ erstellen
Auflösen des Gleichungssystem ergibt die Lotfußpunkte 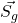$\vec{S_g}$ und $\vec{S_h}$
Bestimmung des Abstands der windschiefen Geraden: $d = \vert \vec{S_g S_h} \vert$

Abstand windschiefer Geraden mit laufenden Punkten, Abstand windschiefer Geraden, Abstand Gerade Gerade, Entfernung zwischen zwei Geraden, Abstandsrechnung — Abstand windschiefer Geraden mit laufenden Punkten

Beispiel „laufender Punkt“

Wir suchen den Abstand der Geraden und .

$g: \vec{x} = \left( \begin{array}{c} 1 \\\ 4 \\\ 2 \\\ \end{array}\right) + \lambda \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right)$

$h: \vec{x} = \left( \begin{array}{c} 3 \\\ 3 \\\ 3 \\\ \end{array}\right) + \phi \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right)$

1. Allgemeinen Verbindungsvektor $\vec{S_g S_h}$ aufstellen

Im ersten Schritt bilden wir die allgemeinen Geradenpunkte („laufende Punkte“) 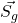$\vec{S_g}$ und $\vec{S_h}$ , deren Koordinaten den Zeilen der Geradengleichungen entsprechen.

$\vec{S_g} = (1 \vert 4 + \lambda \vert 2 + 2\lambda)$

$\vec{S_h} = (3 - \phi \vert 3 + 2\phi \vert 3 + \phi)$

Jetzt können wir den allgemeinen Verbindungsvektor $\vec{S_g S_h}$ berechnen, indem wir $\vec{s_h}$ von $\vec{s_g}$ abziehen.

$\vec{S_g S_h} = \vec{s_h} - \vec{s_g} = \left( \begin{array}{c} 3 - \phi \\\ 3 + 2\phi \\\ 3 + \phi \\\ \end{array}\right) - \left( \begin{array}{c} 1 \\\ 4 + \lambda \\\ 2 + 2\lambda \\\ \end{array}\right)= \left( \begin{array}{c} 2 - \phi \\\ -1 + 2\phi - \lambda \\\ 1 + \phi - 2\lambda \\\ \end{array}\right)$

2. Gleichungssystem aufstellen

Der Verbindungsvektor ist dann am kürzesten, wenn er senkrecht auf den Geraden steht. Den Abstand erhalten wir also zwischen den Punkten, in denen das Skalarprodukt aus $\vec{S_g S_h}$ und den Richtungsvektoren gleich 0 ist. Wir können also folgende zwei Funktionen aufstellen:

$\vec{S_g S_h} \cdot \vec{u} = 0$

$\left( \begin{array}{c} 2 - \phi \\\ -1 + 2\phi - \lambda \\\ 1 + \phi - 2\lambda \\\ \end{array}\right) \cdot \left( \begin{array}{c} 0 \\\ 1 \\\ 2 \\\ \end{array}\right) = 0$

$(2 - \phi) \cdot 0 + (-1 + 2\phi - \lambda) \cdot 1 + (1 + \phi - 2\lambda) \cdot 2 = 0$

$5\lambda - 4 \phi = 1$ (Gleichung I)

$\vec{S_g S_h} \cdot \vec{v} = 0$

$\left( \begin{array}{c} 2 - \phi \\\ -1 + 2\phi - \lambda \\\ 1 + \phi - 2\lambda \\\ \end{array}\right) \cdot \left( \begin{array}{c} -1 \\\ 2 \\\ 1 \\\ \end{array}\right) = 0$

$(2 - \phi) \cdot (-1) + (-1 + 2\phi - \lambda) \cdot 2 + (1 + \phi - 2\lambda) \cdot 1 = 0$

$-4\lambda + 6\phi = 3$ (Gleichung II)

3. Gleichungssystem lösen

Das Gleichungssystem haben wir ja bereits im vorherigen Schritt bestimmt. Es sieht folgendermaßen aus:

I $5\lambda - 4 \phi = 1$
II $-4\lambda + 6\phi = 3$

Hier bietet sich eine Lösung mit Hilfe des Additionsverfahrens an ( $1,5 \cdot I + II$ ).

$3,5\lambda = 4,5$

$\lambda = \frac{9}{7}$

Um den Wert für $\phi$ zu erhalten, müssen wir jetzt dieses $\lambda$ in die Gleichung II einsetzen.

$-4 \cdot \frac{9}{7} + 6 \phi = 3$

$\phi = \frac{19}{14}$

Anschließend können wir die Koordinaten der Lotfußpunkte ermitteln, indem wir diese Ergebnisse in die laufenden Punkte aus Schritt 1 einsetzen.

$\vec{S_g} = (1 \vert 4 + \frac{9}{7} \vert 2 + 2 \cdot \frac{9}{7}) = (1 \vert \frac{37}{7} \vert \frac{32}{7})$

$\vec{S_h} = (3 - \frac{19}{14} \vert 3 + 2 \cdot \frac{19}{14} \vert 3 + \frac{19}{14}) = (\frac{23}{14} \vert \frac{40}{7} \vert \frac{61}{14})$

4. Verbindungsvektor aufstellen und Länge berechnen

Die Lotfußpunkte haben wir jetzt bestimmt. Ziehen wir ihre Vektoren voneinander ab, so erhalten wir den Verbindungsvektor $\vec{S_g S_h}$ .

$\vec{S_g S_h} = \vec{s_h} - \vec{s_g} = \left( \begin{array}{c} \frac{23}{14} \\\\ \frac{40}{7} \\\\ \frac{61}{14} \\\\ \end{array}\right) - \left( \begin{array}{c} 1 \\\\ \frac{37}{7} \\\\ \frac{32}{7} \\\\ \end{array}\right) = \left( \begin{array}{c} \frac{9}{14} \\\\ \frac{3}{7} \\\\ -\frac{3}{14} \\\\ \end{array}\right)$

Der Betrag bzw. die Länge des Verbindungsvektors entspricht dem minimalen Abstand zwischen den windschiefen Geraden.

$d(g, h) = \vert \vec{S_g S_h} \vert = \sqrt{(\frac{9}{14})^2 + \frac{3}{7}^2 + (-\frac{3}{14})^2} \approx 0,8$

Abstandsrechnungen in der Geometrie

Abstände kannst du in der Geometrie zwischen verschiedenen Objekten bestimmen. Zum Glück haben wir zu all diesen Themen eigene Beiträge für dich:

Abstand zwischen zwei Punkten (Abstand zweier Punkte )
Abstand zwischen einem Punkt und einer Geraden (Abstand Punkt Gerade )
Abstand zwischen zwei Geraden (Abstand Gerade Gerade )
- wenn die Geraden parallel verlaufen (Abstand Gerade Gerade )
- wenn die Geraden windschief zueinanderstehen
Abstand zwischen einem Punkt und einer Ebene (Abstand Punkt Ebene )
Abstand zwischen einer Geraden und einer Ebene (Abstand Gerade Ebene )

zur Videoseite: Abstand windschiefer Geraden

Euklidische Distanz

Dreidimensionales Koordinatensystem

Abstand zweier Punkte

Abstand Punkt Gerade

Lagebeziehungen von Geraden

Abstand Gerade Gerade

Abstand Punkt Ebene

Abstand Gerade Ebene

Lotfußpunktverfahren

Abstand windschiefer Geraden

Thema präsentiert von unserem Werbepartner

Zur Webseite

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Bitte .