Chinesischer Restsatz
Dieser Artikel befasst sich mit dem chinesischen Restsatz. Darunter wird im Allgemeinen der chinesische Restsatz für allgemeine Ringe verstanden. Im Speziellen lässt sich der Satz auch für Hauptidealringe wie beispielsweise den ganzen Zahlen formulieren. Auf den chinesischen Restsatz für ganze Zahlen soll in diesem Artikel etwas genauer eingegangen werden. Mithilfe des Satzes wird zunächst aufgezeigt, wie simultane Kongruenzen in verschiedenen Fällen gelöst werden können. Anschließend wird dieses Vorgehen mit Beispielen untermauert.
Das Wichtigste rund um das Thema chinesischer Restsatz haben wir auch noch in einem kurzen Video für dich zusammengefasst. Dadurch sparst du dir Zeit und Lesearbeit und erhältst trotzdem einen guten Überblick über das Thema!
Inhaltsübersicht
Chinesischer Restsatz für allgemeine Ringe
Der chinesische Restsatz trifft eine Aussage über die Isomorphie zwischen einem Faktorring  modulo des Schnittes koprimer Ideale
modulo des Schnittes koprimer Ideale 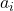 und dem Produkt der Faktorringe
und dem Produkt der Faktorringe  modulo
modulo 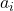 . Für den Ring der ganzen Zahlen lässt sich der chinesische Restsatz anwenden, um simultane Kongruenzen zu lösen.
. Für den Ring der ganzen Zahlen lässt sich der chinesische Restsatz anwenden, um simultane Kongruenzen zu lösen.
Doch hier soll der Satz zunächst einmal für allgemeine Ringe konkret formuliert werden:
Sei  ein Ring und seien
ein Ring und seien  Ideale von
Ideale von  mit der Eigenschaft
mit der Eigenschaft  für alle
für alle  , also paarweise teilerfremde bzw. koprime Ideale. Dann ist die folgende Abbildung ein Isomorphismus:
, also paarweise teilerfremde bzw. koprime Ideale. Dann ist die folgende Abbildung ein Isomorphismus:

Chinesischer Restsatz für Hauptidealringe
Für den Spezialfall, dass der betrachtete Ring  ein Hauptidealring ist, lässt sich der Satz wie folgt formulieren:
ein Hauptidealring ist, lässt sich der Satz wie folgt formulieren:
Sei R ein Hauptidealring und seien  paarweise teilerfremd, d.h. es gilt für alle
paarweise teilerfremd, d.h. es gilt für alle  die Gleichung
die Gleichung  . Dann ist die folgende Abbildung ein Isomorphismus:
. Dann ist die folgende Abbildung ein Isomorphismus:

Äquivalent zu der Forderung, dass für alle  gilt
gilt  , also dass die Ringelemente
, also dass die Ringelemente  paarweise teilerfremd sind, ist die Tatsache, dass für alle
paarweise teilerfremd sind, ist die Tatsache, dass für alle  gilt: „ggT“ (
gilt: „ggT“ ( .
.
Chinesischer Restsatz für ganze Zahlen
Umgemünzt auf den Hauptidealring der ganzen Zahlen lässt sich der chinesische Restsatz folgendermaßen formulieren:
Sind die ganzen Zahlen  paarweise teilerfremd, so ist die folgende Abbildung ein Isomorphismus:
paarweise teilerfremd, so ist die folgende Abbildung ein Isomorphismus:

Der Chinesische Restsatz für ganze Zahlen wird meist in Bezug auf simultane Kongruenzen formuliert.
Simultane Kongruenzen ganzer Zahlen
Mit einer simultanen Kongruenz ganzer Zahlen ist ein System von linearen Kongruenzen gemeint:




Ist diejenige Zahl  gesucht, die zu den vorgegebenen Zahlen
gesucht, die zu den vorgegebenen Zahlen  und
und  eine Lösung der simultanen Kongruenz ist, so trifft der chinesische Restsatz eine Aussage zu dieser Lösung:
eine Lösung der simultanen Kongruenz ist, so trifft der chinesische Restsatz eine Aussage zu dieser Lösung:
Sind die ganzen Zahlen  paarweise teilerfremd, so ist das gegebene System simultaner Kongruenzen
paarweise teilerfremd, so ist das gegebene System simultaner Kongruenzen  mit
mit  für beliebige ganze Zahlen
für beliebige ganze Zahlen  lösbar. Eine Lösung
lösbar. Eine Lösung  dieser Kongruenzen ist dann eindeutig bestimmt modulo
dieser Kongruenzen ist dann eindeutig bestimmt modulo  .
.
Der Beweis dieser Aussage liefert auch gleichzeitig ein Verfahren zur Bestimmung dieser Lösung.
Chinesischer Restsatz: Beweis
Zunächst einmal soll die Existenz einer Lösung  der simultanen Kongruenz gezeigt werden. Hierzu wird mit
der simultanen Kongruenz gezeigt werden. Hierzu wird mit  das Produkt der paarweise teilerfremden Moduln definiert. Weiter wird
das Produkt der paarweise teilerfremden Moduln definiert. Weiter wird 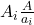 definiert. Aufgrund der Teilerfremdheit der Moduln
definiert. Aufgrund der Teilerfremdheit der Moduln  gilt:
gilt:

Das heißt, es können beispielsweise mit dem erweiterten euklidischen Algorithmus ganze Zahlen  und
und  gefunden werden, sodass gilt:
gefunden werden, sodass gilt:

Es gilt demzufolge für  :
:


Eine Lösung der simultanen Kongruenz ist dann durch

gegeben.
Nun soll gezeigt werden, dass diese Lösung eindeutig modulo  ist. Dazu wird zunächst angenommen, dass y eine weitere Lösung sei. Dann gilt:
ist. Dazu wird zunächst angenommen, dass y eine weitere Lösung sei. Dann gilt:
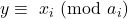
Allerdings gilt auch weiterhin

Daher muss also  kongruent zu
kongruent zu  modulo
modulo  sein. Es gilt also:
sein. Es gilt also:

Das wiederum bedeutet nichts anderes, als dass jedes 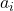 die Differenz zwischen
die Differenz zwischen  und
und  teilt:
teilt:

Da die Moduln 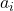 paarweise teilerfremd sind, teilt auch deren Produkt
paarweise teilerfremd sind, teilt auch deren Produkt  die Differenz zwischen
die Differenz zwischen  und
und  :
:

Das heißt die weitere Lösung  der simultanen Kongruenz ist kongruent zur Lösung
der simultanen Kongruenz ist kongruent zur Lösung  modulo
modulo  :
:

Chinesischer Restsatz: Nicht teilerfremde Moduln
Für den Fall, dass die Moduln 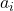 nicht teilerfremd sind, gibt es unter der Voraussetzung, dass für alle
nicht teilerfremd sind, gibt es unter der Voraussetzung, dass für alle  gilt:
gilt:

auch eine Lösung der simultanen Kongruenz. Alle Lösungen sind dann kongruent modulo dem kleinsten gemeinsamen Vielfachen der 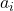 .
.
Eine Lösung lässt sich dann durch sukzessive Substitution von Kongruenzen lösen, bis sich eine simultane Kongruenz mit paarweise teilerfremden Moduln ergibt. Dieses lässt sich dann wie im Beweis des Restsatzes gezeigt lösen. Wie die sukzessive Substitution erfolgt, soll später an einem konkreten Beispiel gezeigt werden.
Chinesischer Restsatz Beispiel
Zunächst soll allerdings ein Beispiel durchgerechnet werden, bei dem die Moduln teilerfremd sind.
Beispiel: Chinesischer Restsatz teilerfremde Moduln
Gesucht sei eine ganze Zahl  mit der Eigenschaft:
mit der Eigenschaft:



Zum Finden einer Lösung wird nun die Argumentationskette des Beweises abgearbeitet. Zunächst wird das Produkt der teilerfremden Moduln gebildet:

Somit lauten die  ∶
∶



Mit dem erweiterten euklidischen Algorithmus lassen sich ganze Zahlen  und
und  mit
mit  finden:
finden:



Es gilt also für 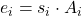 :
:



Weiterhin gilt:



Eine Lösung der simultanen Kongruenz lautet demnach

Aufgrund der Tatsache  sind also alle Lösungen kongruent zu 47 modulo 60.
sind also alle Lösungen kongruent zu 47 modulo 60.
Beispiel: Chinesischer Restsatz nicht teilerfremde Moduln
Als Beispiel einer simultanen Kongruenz nicht teilerfremder Moduln soll folgendes System betrachtet werden:






Hier sind nun einige Kongruenzaussagen redundant. Diese lassen sich finden, indem die Moduln als Produkt von Primzahlpotenzen geschrieben werden. Es folgt:






Die Kongruenzaussage  ist äquivalent dazu, dass
ist äquivalent dazu, dass  und
und  gilt. Das System ist also äquivalent zu:
gilt. Das System ist also äquivalent zu:







Hier sind nun einige Forderungen doppelt genannt. Außerdem ist  eine Forderung, welche die Forderung
eine Forderung, welche die Forderung  bereits beinhaltet. Daher vereinfacht sich das System zu:
bereits beinhaltet. Daher vereinfacht sich das System zu:




In diesem System treten nur paarweise teilerfremde Moduln auf und es lässt sich somit auf bekannte Art und Weise lösen.
