Rotationskörper
In diesem Beitrag erklären wir dir, was Rotationskörper sind und wie du sie berechnest. Am besten kannst du dir die Rotationskörper bildlich vorstellen, wenn du dir unser Video anschaust.
Inhaltsübersicht
Rotationskörper einfach erklärt
Was ein Rotationskörper ist, kannst du dir leicht vorstellen, wenn du berücksichtigst, wie er entsteht. Dazu betrachtest du eine Fläche im Koordinatensystem (z.B. ein Dreieck) und drehst diese Fläche um  um eine der beiden Koordinatenachsen. Die dreidimensionale Figur, die dadurch entsteht, heißt Rotationskörper. Im Falle eines Dreiecks erhältst du einen Kegel.
um eine der beiden Koordinatenachsen. Die dreidimensionale Figur, die dadurch entsteht, heißt Rotationskörper. Im Falle eines Dreiecks erhältst du einen Kegel.
Ein Rotationskörper kann sehr verschiedene Formen annehmen. Das hängt einerseits von der rotierenden Fläche ab und andererseits davon, um welche Achse das Flächenstück rotiert. War deine ursprüngliche Fläche beispielsweise ein Rechteck, erhältst du einen Zylinder.
Rotationskörper Formel
Zunächst wollen wir uns anschauen, wie du das Volumen von einem Rotationskörper berechnen kannst. Dabei macht es einen Unterschied, ob der Körper um die x-Achse oder um die y-Achse gedreht wird. Wir betrachten die beiden Formeln unabhängig voneinander und schauen uns zuerst die Rotation um die x-Achse an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Volumen Rotationskörper bei Drehung um die x-Achse
Wenn du eine Kurve  gegeben hast, die mit der x-Achse und der y-Achse ein Flächenstück einschließt, erhältst du durch Drehung um die x-Achse einen Rotationskörper. Sein Volumen
gegeben hast, die mit der x-Achse und der y-Achse ein Flächenstück einschließt, erhältst du durch Drehung um die x-Achse einen Rotationskörper. Sein Volumen  kannst du mittels Integration und der folgenden Formel berechnen.
kannst du mittels Integration und der folgenden Formel berechnen.

Die Integrationsgrenzen  und
und  sind die x-Werte, die dein Flächenstück begrenzen, d.h. die Grenzen deines Definitionsbereichs
von
sind die x-Werte, die dein Flächenstück begrenzen, d.h. die Grenzen deines Definitionsbereichs
von  . Aber Vorsicht! Rotiert dein Flächenstück um die y-Achse, brauchst du eine andere Formel!
. Aber Vorsicht! Rotiert dein Flächenstück um die y-Achse, brauchst du eine andere Formel!
Rotationskörper Volumen bei Drehung um die y-Achse
Rotiert dein Flächenstück um die y-Achse, so berechnest du den Rotationskörper anders. Genauer gesagt gibt es zwei verschiedene Möglichkeiten, die aber auf dasselbe Ergebnis führen. Weil du hier die Umkehrfunktion
 benötigst, ist es wichtig, dass
benötigst, ist es wichtig, dass  stetig und monoton ist!
stetig und monoton ist!

Dabei sind  und
und  dieses Mal die Grenzen deines Wertebereichs
, also die Werte, die du erhältst, wenn du die untere und die obere Integrationsgrenze in
dieses Mal die Grenzen deines Wertebereichs
, also die Werte, die du erhältst, wenn du die untere und die obere Integrationsgrenze in  einsetzt. Die zweite Möglichkeit der Berechnung lautet
einsetzt. Die zweite Möglichkeit der Berechnung lautet

Mantelfläche bei Rotation um x-Achse
Zur Berechnung der Mantelfläche benötigst du bei der Rotation um die x-Achse diese Formel:

Mantelfläche bei Rotation um y-Achse
Für die Rotation um die y-Achse brauchst du wieder die Umkehrfunktion  . Die zugehörige Formel lautet dann
. Die zugehörige Formel lautet dann

Rotationskörper berechnen: Beispiele
Damit du noch besser verstehst, wie du Volumen und Mantelfläche von einem Rotationskörper berechnest, betrachten wir nun einige Beispiele.
Beispiel 1: Rotationsvolumen bei Drehung um die x-Achse
Gesucht sei das Rotationsvolumen von  im Intervall
im Intervall ![Rendered by QuickLaTeX.com \left[0, 2\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-75786f38367cc1608f41ba94a1a4a2bd_l3.png) bei Rotation um die x-Achse. Gegeben ist die Funktion
bei Rotation um die x-Achse. Gegeben ist die Funktion  , die im Intervall
, die im Intervall ![Rendered by QuickLaTeX.com \left[0,2\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ec08abd53e2402161bfb875102cf307d_l3.png) ein Flächenstück beschreibt. Gesucht ist das Volumen des Rotationskörpers, der durch Drehung des Flächenstücks um die x-Achse entsteht. Dazu müssen wir nur alle Werte in die obige Formel für die Rotation um die x-Achse einsetzen und berechnen
ein Flächenstück beschreibt. Gesucht ist das Volumen des Rotationskörpers, der durch Drehung des Flächenstücks um die x-Achse entsteht. Dazu müssen wir nur alle Werte in die obige Formel für die Rotation um die x-Achse einsetzen und berechnen


![Rendered by QuickLaTeX.com = \pi \left[ \frac{1}{20}x^5+\frac{1}{3}x^3+x\right]\limites_0^2](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-aa50cc0173c9e057660da2d8077f4b93_l3.png)

Beispiel 2: Rotationsvolumen bei Drehung um die y-Achse
Gesucht sei das Rotationsvolumen von  im Intervall
im Intervall ![Rendered by QuickLaTeX.com \left[0, 2\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-75786f38367cc1608f41ba94a1a4a2bd_l3.png) bei Rotation um die y-Achse. Damit du den Unterschied zwischen der Drehung um die x-Achse und der Drehung um die y-Achse direkt siehst, betrachten wir noch einmal dieselbe Funktion wie im ersten Beispiel. Drehst du sie um die y-Achse erhältst du einen ganz anderen Körper! Sein Volumen wollen wir nun auf die beiden möglichen Arten bestimmen. Um die erste Formel anwenden zu können, benötigen wir jedoch zuerst die Umkehrfunktion
bei Rotation um die y-Achse. Damit du den Unterschied zwischen der Drehung um die x-Achse und der Drehung um die y-Achse direkt siehst, betrachten wir noch einmal dieselbe Funktion wie im ersten Beispiel. Drehst du sie um die y-Achse erhältst du einen ganz anderen Körper! Sein Volumen wollen wir nun auf die beiden möglichen Arten bestimmen. Um die erste Formel anwenden zu können, benötigen wir jedoch zuerst die Umkehrfunktion  . Diese ist in
. Diese ist in ![Rendered by QuickLaTeX.com [0,2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) wohldefiniert, da
wohldefiniert, da  in diesem Intervall streng monoton steigend ist. Aber Vorsicht: Im Allgemeinen gilt das nicht! Wir berechnen die Umkehrfunktion, indem wir
in diesem Intervall streng monoton steigend ist. Aber Vorsicht: Im Allgemeinen gilt das nicht! Wir berechnen die Umkehrfunktion, indem wir  nach
nach  auflösen
auflösen


Um das Rotationsvolumen auszurechnen, fehlen jetzt noch die Integralgrenzen. Dazu berechnen wir  und
und  und erhalten
und erhalten


![Rendered by QuickLaTeX.com = \pi \cdot \left[y^2-2y\right]\limits_1^3](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-86b69c86aee52b0a94697125db91d98a_l3.png)

Zur Überprüfung wollen wir das Volumen auch noch mit der zweiten Formel bestimmen. Dazu benötigen wir die Ableitung  . Einsetzen ergibt
. Einsetzen ergibt

Die Betrag-Striche kannst du hier weglassen, weil  in
in ![Rendered by QuickLaTeX.com [0,2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) positiv ist. Also gilt
positiv ist. Also gilt


![Rendered by QuickLaTeX.com = \pi \cdot \left[ \frac{1}{4}x^4\right]\limits_0^2 = 4\pi.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fab7c70aaa403a0ced69f2820da934d7_l3.png)
Achtung: Pass auf, dass du das  bei der Berechnung nirgends vergisst!
bei der Berechnung nirgends vergisst!
Beispiel 3: Mantelfläche Rotationskörper um die x-Achse
Sei  die Funktion, die im Intervall
die Funktion, die im Intervall ![Rendered by QuickLaTeX.com [0,2]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) durch Rotation um die x-Achse einen Kegel beschreibt. Seine Mantelfläche lässt sich mit obiger Formel leicht berechnen. Dazu musst du zuerst die Ableitung
durch Rotation um die x-Achse einen Kegel beschreibt. Seine Mantelfläche lässt sich mit obiger Formel leicht berechnen. Dazu musst du zuerst die Ableitung  bestimmen und in die Formel einsetzen
bestimmen und in die Formel einsetzen


![Rendered by QuickLaTeX.com = 2\pi \cdot \sqrt{5} \biggl[ -x^2+4x\biggr]\limits_0^2 = 8\pi \cdot \sqrt{5}.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1300b061b9bf125206408df017a9c1bc_l3.png)
Beispiel 4: Zusammengesetzte Rotationskörper
In vielen Aufgaben musst du das Volumen eines zusammengesetzten Rotationskörpers berechnen. Das typische Beispiel ist ein Zylinder mit aufgesetztem Kegel. Das Volumen dieses Rotationskörpers kannst du bestimmen, indem du zuerst das Volumen des Zylinders ausrechnest, und dann das Volumen des Kegels addierst. In der Abbildung siehst du die Rotationsfläche, die durch  in
in ![Rendered by QuickLaTeX.com [0,3]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d71bbe09eb56b05f6dfc23448da8487f_l3.png) und
und  in
in ![Rendered by QuickLaTeX.com [3,5]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a726c502fc123000f7d5c0fbea51cb62_l3.png) beschrieben wird. Willst du das zugehörige Rotationsvolumen bestimmen, berechnest du also
beschrieben wird. Willst du das zugehörige Rotationsvolumen bestimmen, berechnest du also

![Rendered by QuickLaTeX.com = \pi \cdot \biggl[4x\biggr]\limits_0^3 + \pi \left[\frac{1}{3}x^3-5x^2+25x\right]\limits_3^5](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5fb7743bf049c78806262100a3b873fd_l3.png)

Rotationskörper Aufgaben
Wenn du selbstständig weiter üben möchtest, findest du hier noch einige etwas schwerere Aufgaben mit Lösungen. Aufgabe 1 Sei  eine Funktion, die durch Rotation um die x-Achse im Intervall
eine Funktion, die durch Rotation um die x-Achse im Intervall ![Rendered by QuickLaTeX.com [0,9]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2a42aa9c65ebe970607dacd9c9f420a8_l3.png) eine Schüssel beschreibt. Werden
eine Schüssel beschreibt. Werden  und
und  in
in  angegeben, so ist die Schüssel
angegeben, so ist die Schüssel  hoch. a) Skizziere den Rotationskörper und berechne dann den Durchmesser der Schüssel. b) Welches Volumen hat die Schüssel? Wie viele Liter sind das? Aufgabe 2
hoch. a) Skizziere den Rotationskörper und berechne dann den Durchmesser der Schüssel. b) Welches Volumen hat die Schüssel? Wie viele Liter sind das? Aufgabe 2  rotiert um die y-Achse. Das Volumen des zugehörigen Rotationskörpers soll
rotiert um die y-Achse. Das Volumen des zugehörigen Rotationskörpers soll  betragen. Berechne die möglichen Integrationsgrenzen, wenn eine Einheit einem Zentimeter entspricht.
betragen. Berechne die möglichen Integrationsgrenzen, wenn eine Einheit einem Zentimeter entspricht.
Lösungen:
Aufgabe 1: a) Um den Durchmesser von diesem Rotationskörper zu berechnen, setzt du lediglich die obere Grenze des Definitionsbereiches in  ein und erhältst für den Radius
ein und erhältst für den Radius
 .
.
Der Durchmesser beträgt somit  . b) Setzt du alle Parameter in die Formel zur Berechnung des Volumens bei Rotation um die x-Achse ein, musst du das Integral
. b) Setzt du alle Parameter in die Formel zur Berechnung des Volumens bei Rotation um die x-Achse ein, musst du das Integral

berechnen. Als Lösung erhältst du dann
 .
.
Aufgabe 2: Um die Integrationsgrenzen zu bestimmen, setzt du alle bekannten Werte in die Formel für den Rotationskörper bei Drehung um die y-Achse ein:

![Rendered by QuickLaTeX.com \Longleftrightarrow 16 = \biggl[\frac{1}{2}x^5 \biggr]\limits_a^b.](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dd0f8b34d835588206e3e1afbf2c8e89_l3.png)
Wähle nun  und erhalte dann
und erhalte dann 
Rotationskörper — häufigste Fragen
(ausklappen)
Rotationskörper — häufigste Fragen
(ausklappen)-
Wie erkenne ich, ob ich Scheibenmethode oder Schalenmethode brauche?Du brauchst die Scheibenmethode, wenn du senkrecht zur Drehachse integrierst, und die Schalenmethode, wenn du parallel zur Drehachse integrierst. Bei Rotation um die x-Achse ist die Scheibenmethode meist
 .
.
-
Welche Fehler passieren oft bei den Integralgrenzen bei Rotation?Häufige Fehler bei Integralgrenzen sind, dass bei Rotation um die y-Achse fälschlich
 bis
bis  statt
statt  bis
bis  verwendet wird. Das liegt daran, dass dann nach
verwendet wird. Das liegt daran, dass dann nach  integriert wird und die Grenzen aus dem Wertebereich kommen. Beispiel: Bei
integriert wird und die Grenzen aus dem Wertebereich kommen. Beispiel: Bei ![Rendered by QuickLaTeX.com [0,2]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) ist
ist  und
und  , also
, also  statt
statt  .
.
-
Wann muss ich bei der Umkehrfunktion den richtigen Ast wählen?Den richtigen Ast der Umkehrfunktion musst du wählen, sobald beim Auflösen eine
 -Wurzel entsteht. Entscheidend ist, welcher x-Bereich im betrachteten Intervall wirklich vorkommt, damit
-Wurzel entsteht. Entscheidend ist, welcher x-Bereich im betrachteten Intervall wirklich vorkommt, damit  eindeutig bleibt. Beispiel: Aus
eindeutig bleibt. Beispiel: Aus  folgt
folgt  , aber auf
, aber auf ![Rendered by QuickLaTeX.com [0,2]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-c6cc9e42627fb0516082896ece53b0b3_l3.png) gilt nur
gilt nur  .
.
-
Wie berechne ich das Volumen, wenn die Fläche nicht an der Achse liegt?Liegt die Fläche nicht an der Drehachse, rechnest du mit Außenradius minus Innenradius (Washer-Methode):
 . Der Innenradius
. Der Innenradius  ist der Abstand zur Achse, der nicht „mitgedreht“ werden soll. Beispiel: Zwischen
ist der Abstand zur Achse, der nicht „mitgedreht“ werden soll. Beispiel: Zwischen  und
und  um die x-Achse gilt
um die x-Achse gilt  und
und  .
.
-
Wie gehe ich vor, wenn f(x) im Intervall nicht monoton ist?Wenn
 im Intervall nicht monoton ist, musst du das Intervall in Teilintervalle zerlegen, in denen
im Intervall nicht monoton ist, musst du das Intervall in Teilintervalle zerlegen, in denen  monoton ist. Nur dann ist eine Umkehrfunktion pro Teilstück eindeutig und die y-Achsen-Formel mit
monoton ist. Nur dann ist eine Umkehrfunktion pro Teilstück eindeutig und die y-Achsen-Formel mit  funktioniert sauber. Beispiel: Teile bei einem Hochpunkt
funktioniert sauber. Beispiel: Teile bei einem Hochpunkt  in
in ![Rendered by QuickLaTeX.com [a,c]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-dca626590cacda59fc5e751bc6014f49_l3.png) und
und ![Rendered by QuickLaTeX.com [c,b]](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-57477c3c5c9f05a8f4973630cc55001f_l3.png) und berechne die Volumina getrennt, dann addierst du sie.
und berechne die Volumina getrennt, dann addierst du sie.
Integralrechnung
Damit du das Volumen und die Mantelfläche eines Rotationskörpers ermitteln kannst, musst du unbedingt die Integralrechnung verstehen. Schau dir nochmal unser Video dazu an, damit du Rotationskörper in deiner Prüfung problemlos berechnen kannst!

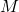 berechnen. Bei einem
berechnen. Bei einem 
