Koordinatenform
In diesem Artikel zeigen wir dir, was die Koordinatenform einer Gerade oder Ebene ist. Du möchtest das Thema lieber in visueller Form sehen? Dann schau dir unser Video dazu an!
Inhaltsübersicht
Koordinatenform einfach erklärt
Die Koordinatenform ist eine Darstellung von Geraden oder Ebenen. Damit kannst du sehr leicht überprüfen, ob ein Punkt auf einer Gerade oder einer Ebene liegt.
Für eine Gerade gilt

und für eine Ebene ist
 .
.
Dabei sind a, b, c und d beliebige Zahlen.
Bemerkung: Die Koordinatenform ist nichts anderes, als die ausmultiplizierte Form der Normalenform
. Außerdem kannst du Geraden und Ebenen auch mit der Parameterform
darstellen.
Koordinatenform Gerade
Du kannst jede Gerade  mit der Koordinatenform darstellen.
mit der Koordinatenform darstellen.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Eine Gerade  wird zum Beispiel durch die Koordinatenform
wird zum Beispiel durch die Koordinatenform

dargestellt. Möchtest du nun überprüfen, ob ein Punkt  auf der Gerade liegt, dann setzt du lediglich die Komponenten des Punktes in die Form ein und schaust, ob die Gleichung erfüllt wird.
auf der Gerade liegt, dann setzt du lediglich die Komponenten des Punktes in die Form ein und schaust, ob die Gleichung erfüllt wird.
So liegt zum Beispiel der Punkt  auf der Gerade
auf der Gerade  , denn
, denn
 .
.
Der Punkt  hingegen liegt nicht auf der Gerade, da
hingegen liegt nicht auf der Gerade, da
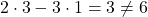 .
.
Beispiel
Die Koordinatenform

beschreibt eine Ebene im  . Um nun zu überprüfen, ob ein Punkt auf der Ebene liegt, setzt du die Komponenten des Punktes in die Koordinatenform der Ebene ein und schaust, ob die Gleichung erfüllt ist.
. Um nun zu überprüfen, ob ein Punkt auf der Ebene liegt, setzt du die Komponenten des Punktes in die Koordinatenform der Ebene ein und schaust, ob die Gleichung erfüllt ist.
Der Punkt  liegt zum Beispiel auf der Ebene, da
liegt zum Beispiel auf der Ebene, da
 .
.
Aber der Punkt  liegt nicht auf der Ebene, denn
liegt nicht auf der Ebene, denn
 .
.
Koordinatenform — häufigste Fragen
(ausklappen)
Koordinatenform — häufigste Fragen
(ausklappen)-
Was ist die Koordinatenform bei einer Gerade oder Ebene?Die Koordinatenform beschreibt eine Gerade als
 und eine Ebene als
und eine Ebene als  . Dabei sind
. Dabei sind  beliebige reelle Zahlen. Mit dieser Gleichung kannst du direkt rechnen und zum Beispiel prüfen, ob ein Punkt die Gleichung erfüllt.
beliebige reelle Zahlen. Mit dieser Gleichung kannst du direkt rechnen und zum Beispiel prüfen, ob ein Punkt die Gleichung erfüllt.
-
Wie prüfe ich mit der Koordinatenform, ob ein Punkt auf einer Gerade liegt?Du setzt die Koordinaten des Punkts in
 ein und prüfst, ob die Gleichung stimmt. Ist links genau
ein und prüfst, ob die Gleichung stimmt. Ist links genau  , dann liegt der Punkt auf der Geraden; sonst nicht. Beispiel: Bei
, dann liegt der Punkt auf der Geraden; sonst nicht. Beispiel: Bei  liegt
liegt  darauf, denn
darauf, denn  .
.
-
Wie prüfe ich mit der Koordinatenform, ob ein Punkt auf einer Ebene liegt?Setze die drei Koordinaten des Punkts in
 ein und kontrolliere, ob das Ergebnis
ein und kontrolliere, ob das Ergebnis  ist. Wenn die Gleichung erfüllt ist, liegt der Punkt auf der Ebene. Beispiel: Auf
ist. Wenn die Gleichung erfüllt ist, liegt der Punkt auf der Ebene. Beispiel: Auf  liegt
liegt  , weil
, weil  .
.
-
Was sagt es über eine Gerade aus, wenn a oder b oder c in der Koordinatenform 0 ist?Bei
 bedeutet
bedeutet  , dass die Gerade parallel zur x-Achse verläuft, und
, dass die Gerade parallel zur x-Achse verläuft, und  , dass sie parallel zur y-Achse ist. Ist
, dass sie parallel zur y-Achse ist. Ist  , dann geht die Gerade durch den Ursprung. Diese Sonderfälle erkennst du direkt am jeweiligen Koeffizienten.
, dann geht die Gerade durch den Ursprung. Diese Sonderfälle erkennst du direkt am jeweiligen Koeffizienten.
-
Was sagt es über eine Ebene aus, wenn a oder b oder c oder d in der Koordinatenform 0 ist?In
 heißt
heißt  , dass die Ebene parallel zur
, dass die Ebene parallel zur  -Achse ist, bei
-Achse ist, bei  parallel zur
parallel zur  -Achse und bei
-Achse und bei  parallel zur
parallel zur  -Achse. Ist
-Achse. Ist  , dann geht die Ebene durch den Ursprung.
, dann geht die Ebene durch den Ursprung.
Koordinatenform Aufgabe
Überprüfe, ob die folgenden Punkte auf der Ebene  liegen.
liegen.
a) 
b) 
Lösung
Um zu überprüfen, ob die Punkte auf der Ebene liegen, setzt du die Komponenten der Punkte in die Form ein und schaust, ob du dabei  erhältst.
erhältst.
a)  .
.
Der Punkt  liegt demnach auf der Ebene.
liegt demnach auf der Ebene.
b)  .
.
Also liegt der Punkt  nicht auf der Ebene.
nicht auf der Ebene.
 , dann ist die Gerade
, dann ist die Gerade  verläuft die Gerade
verläuft die Gerade  , dann geht die Gerade
, dann geht die Gerade  schneidet die Gerade
schneidet die Gerade  und
und  .
.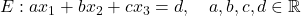
 und
und  findest du auch manchmal die Bezeichnung
findest du auch manchmal die Bezeichnung  .
. , so verläuft die Ebene parallel zur
, so verläuft die Ebene parallel zur  -Achse.
-Achse. ist die Ebene parallel zur
ist die Ebene parallel zur  -Achse.
-Achse. , dann ist die Ebene parallel zur
, dann ist die Ebene parallel zur  , so geht die Ebene durch den Ursprung.
, so geht die Ebene durch den Ursprung. , dann schneidet die Ebene die Achsen bei
, dann schneidet die Ebene die Achsen bei  ,
,  und
und 